线性回归(linear regression)
算法介绍
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。线性回归按自变量的个数分为2种:
- 简单线性回归:只有一个自变量
- 多元线性回归:自变量的个数大于等于两个
基本形式
在一般情况下,假设有$p$个自变量,$y$为因变量,设:
$$
y=\beta_0+\beta_1x_1+\cdots+\beta_px_p
$$
在模型构建过程中,利用 $y$ 与 $x_1, \cdots, x_p$ 的训练数据来估计$\beta_0$与$\beta_1, \cdots, \beta_p$得到:
$$
\hat{y}=\hat{\beta_0}+\hat{\beta_1}x_1+\cdots+\hat{\beta_p}x_p\
$$
$$
\hat{y}=\left[
\begin{matrix}
1 & x_1 & \cdots & x_p\
\end{matrix}
\right]
\left[
\begin{matrix}
\hat{\beta_0} \
\vdots \
\hat{\beta_p}
\end{matrix}
\right]=X*W(W是列向量)
$$
拟合方程
线性回归的损失函数一般由最小二乘法求得
最小二乘法(ordinary least squares)
最小二乘法的主要思想是通过确定未知参数(通常是一个参数矩阵),来使得真实值和预测值的误差(也称残差)平方和最小,其计算公式为:
$$
E=\sum_{i=1}^n(y_i-\hat{y_i})^2
$$
其中$y_i$是真实值,$\hat{y_i}$是对应的预测值,图示如下:(橙色线即为误差)
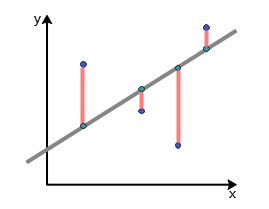
损失函数
由最小二乘法可得线性回归得损失函数为:
$$
J(W)=\sum_{i=1}^n(y_i-\hat{y_i})^2=\sum_{i=1}^n(y_i-X_i*W)^2
$$
要使得损失函数最小,可以将损失函数作为多元函数处理,下面给出一维特征(自变量仅有一个的情况)的损失函数最小求解:(设线性回归方程为:$\hat{y}=\hat{\beta_0}+\hat{\beta_1}x$)
$$
\hat{\beta_0}=\frac{\sum_{i=1}^{m}\left(x^{(i)}\right)^{2} \sum_{i=1}^{m} y^{(i)}-\sum_{i=1}^{m} x^{(i)} \sum_{i=1}^{m} x^{(i)} y^{(i)}}{m \sum_{i=1}^{m}\left(x^{(i)}\right)^{2}-\left(\sum_{i=1}^{m} x^{(i)}\right)^{2}}
$$
$$
\hat{\beta_1}=\frac{m\sum\limits_{i=1}^{m}x^{(i)}y^{(i)}-\sum\limits_{i=1}^{m}x^{(i)}\sum\limits_{i=1}^{m}y^{(i)}}{m\sum\limits_{i=1}^{m}(x^{(i)})^2-(\sum\limits_{i=1}^{m}x^{(i)})^2}
$$
拟合效果检验
线性回归一般利用可决系数$R^2$来反映直线的拟合程度,取值范围在[0,1]之间。$R^2\to1$说明回归方程拟合的越好,$R^2\to0$就代表回归方程拟合的越差,其计算公式如下:
$$
R^2=\frac{\Sigma(\hat y-\overline y)^2}{\Sigma(y-\overline y)^2}
$$