差分和前缀和
|字数总计:2.5k|阅读时长:10分钟|阅读量:
由于昨天学校OJ平台的一次训练赛中出现了一个前缀和差分的题目,本蒟蒻不太会T_T,所以打算系统学习一下前缀和差分的知识点。在文章的最后笔者也会放上那道题的题目以及AC代码。
前缀和
一维前缀和
前缀和可以简单的理解为某个数组中前n项的和,是一种重要的预处理方式,能大大降低查询的时间复杂度。而一维的前缀和比较简单就不做过多的赘述,直接通过一个例子来了解:
给定一个n个元素的数组,要求计算出q次查询中给定的区间的元素的和
对于这个例子可能刚开始最简单的想法就是遍历每次查询的区间求和,但是这种做法在数组元素、查询次数足够多的情况下其时间复杂度就会很高,因此就要用到前缀和的思想。
首先先定义一个数组sum[N],sum[i]表示的是数组索引为0 - i的元素的和,然后假设查询的区间为[L , R]那么该区间和就为sum[R]-sum[L-1](若L==0则区间和为sum[R])
sum[i]的值
当i为0时,sum[i]=arr[0];当i大于0时,sum[i]=sum[i-1]+arr[i]。
下面是演示代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include<iostream>
using namespace std;
const int N = 1e4 + 10;
int arr[N], sum[N], n, q, l, r;
int main(void) {
cin >> n;
for (int i = 0; i < n; ++i)
cin >> arr[i];
sum[0] = arr[0];
for (int i = 1; i < n; ++i)
sum[i] = sum[i - 1] + arr[i];
cin >> q;
while (q--)
{
cin >> l >> r;
if (l == 0) cout << sum[r] << endl;
else cout << sum[r] - sum[l - 1] << endl;
}
return 0;
}
|
运行结果如下:

二维前缀和
对于二维前缀和,其实就是类似求存储在某个二维数组中某个矩阵方块内的数组元素的和,下面以一个二维数组的例子来讲解
1
2
3
4
5
| int arr[3][4]={
{1,5,6,8},
{9,6,7,3},
{5,3,2,4}
};
|
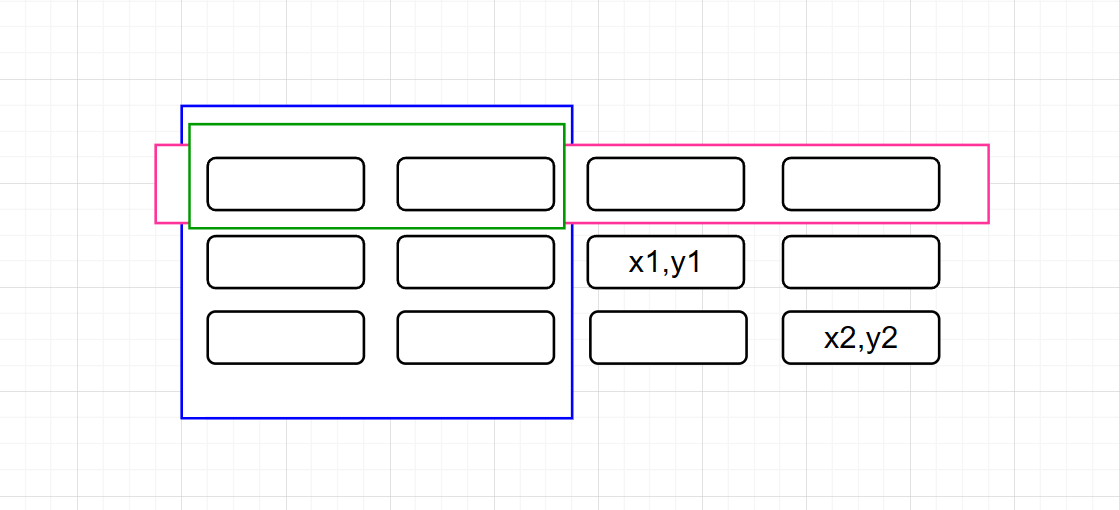
同样先定义一个二维数组sum,sum[ i ] [ j ]的意义为以(0,0)为左上角,(i , j)为右下角构成的矩阵所包含的元素的和(以例子中的二维数组为例,sum[1] [2]就是元素1、5、6、9、6、7元素的和);那么假设所要查询的矩阵是以(x1,y1)、(x2,y2)分别为左上角的点和右下角的点构成的,设查询的结果为sum{x1,y1}{x2,y2},以下图为例来说,sum{x1,y1}{x2,y2}的结果就是sum[ x2 ] [ y2 ]的值减去蓝色框内的再减去红色框内的最后加上绿色框内的重合部分即可,用式子来表示即为(下面式子是所查询的矩阵不包含第一行和第一列的情况,若包含同样的利用方块相减的思路):
sum[x2] [y2] - sum[x2] [y1 - 1] - sum[x1 - 1] [y2] + sum[x1 - 1] [y1 - 1]
sum[ i ] [ j ]的值
- 当i==0且j==0时,sum[ i ] [ j ]=arr[0] [0]
- 当i==0且j != 0时,sum[ i ] [ j ]=sum[ i ] [ j-1 ] + arr[ i ] [ j ]
- 当i != 0且j==0时,sum[ i ] [ j ]=sum[ i-1 ] [ j ] + arr[ i ] [ j ]
- 当i != 0 且j != 0时,sum[ i ] [ j ]=sum[ i ] [ j-1 ]+sum[ i-1 ] [ j ]-sum[ i-1 ] [ j-1 ]+arr[ i ] [ j ]
下面是演示代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include<iostream>
using namespace std;
const int n = 3, m = 4;
int arr[n][m] = {
{1,5,6,8},
{9,6,7,3},
{5,3,2,4}
};
int sum[n][m];
void pre_sum() {
sum[0][0] = arr[0][0];
for (int i = 1; i < n; ++i) sum[i][0] = sum[i - 1][0] + arr[i][0];
for (int i = 1; i < m; ++i) sum[0][i] = sum[0][i - 1] + arr[0][i];
for (int i = 1; i < n; ++i)
for (int j = 1; j < m; ++j)
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + arr[i][j];
}
int get_sum(int x1, int y1, int x2, int y2) {
if (!x1 && !y1) return sum[x2][y2];
if (!x1) return sum[x2][y2] - sum[x2][y1 - 1];
if (!y1) return sum[x2][y2] - sum[x1 - 1][y2];
return sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1];
}
int main(void) {
pre_sum();
cout << get_sum(1, 1, 2, 2) << endl;
cout << get_sum(0, 1, 1, 3) << endl;
return 0;
}
|
差分
一维差分
差分是一种和前缀和相对的策略,可以当作是求和的逆运算。它可以维护多次对序列的一个区间加上一个数,并在最后询问改变后的序列的数。下面以我们学校OJ平台的一道差分模板题来讲述:
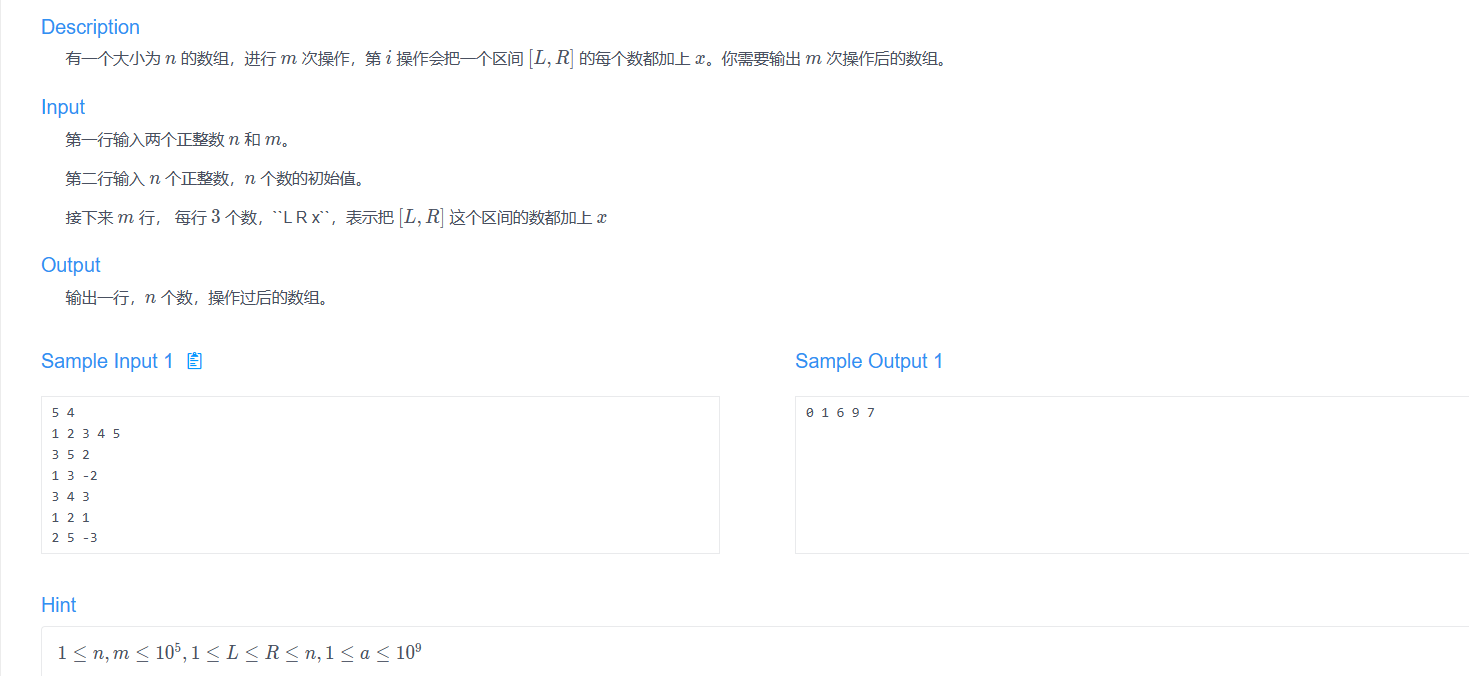
对于这道题如果直接就是每次遍历区间再进行加数的处理,那时间复杂度是O(mn)看了一下m、n最大可以达到1e5,那最后的结果肯定会TLE(因为那时我刚开始就是那样做的hhh,那次也是第一次接触差分)
言归正传,用差分的方法来做这道题,首先定义一个数组arr[N]来存储原始数据,然后还要定义一个数组d[N]。对于数组d的元素,当i==0时,d[i]=arr[i];当i>=0时,d[i]=arr[i]-arr[i-1];我们可以发现原数组arr其实是数组d的前缀和,这也是为什么说差分是一种和前缀和相对的策略;当想使区间[L,R]上的数都加上x时,只需要d[L]+=x,d[R+1]-=x即可。因为当d[L]+=x后,对于数组d的更新后的前缀和数组即arr来说,索引>=L的元素都会加上x,而d[R+1]-=x的作用是使得arr数组中索引为>=(R+1)的元素都减去x,那么最后的结果就是区间[L,R]的元素都加上x,这样执行区间修改操作的时间复杂度就只有O(m)
下面是题目的AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include<iostream>
using namespace std;
typedef long long ll;
const int N = 100005;
ll n, m, l, r, x, arr[N], d[N];
int main(void) {
cin >> n >> m;
for (ll i = 1; i <= n; ++i)
{
cin >> arr[i];
d[i] = arr[i] - arr[i - 1];
}
for (ll i = 0; i < m; ++i)
{
cin >> l >> r >> x;
d[l] += x;
d[r + 1] -= x;
}
for (int i = 1; i <= n; ++i)
{
arr[i] = arr[i - 1] + d[i];
cout << arr[i] << " ";
}
return 0;
}
|
二维差分
对于二维差分同样使用二维前缀和的那个例子中的数组来讲述:
1
2
3
4
5
| int arr[3][4]={
{1,5,6,8},
{9,6,7,3},
{5,3,2,4}
};
|
使用二维差分对该数组某个以(x1,y1)、(x2,y2)分别为左上角的点和右下角的点构成的矩阵内的元素进行修改,首先定义二维的差分数组d来记录修改(d初始化为0),假设对以(x1,y1)、(x2,y2)分别为左上角的点和右下角的点构成的矩阵内的元素同时加上value,那么可以使d[x1] [y1]+=value,d[x2+1] [y1]-=value,d[x1] [y2+1]-=value,d[x2+1] [y2+1]+=value,然后对二维数组d进行二维前缀和的处理即可得到原数组对应位置元素的改变值,执行d[x2+1] [y2+1]+=value操作是因为进行前缀和处理时以(x2+1,y2+1)为左上角顶点的矩阵内的元素被多减去了一个value;结果如下图所示:

代码演示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include<iostream>
using namespace std;
const int n = 3, m = 4;
int arr[n][m] = {
{1,5,6,8},
{9,6,7,3},
{5,3,2,4}
};
int d[5][5], sum[5][5];
void add(int x1, int y1, int x2, int y2, int val) {
d[x1][y1] += val;
d[x2 + 1][y1] -= val;
d[x1][y2 + 1] -= val;
d[x2 + 1][y2 + 1] += val;
}
void pre_sum() {
sum[0][0] = d[0][0];
for (int i = 1; i < n; ++i) sum[i][0] = sum[i - 1][0] + d[i][0];
for (int i = 1; i < m; ++i) sum[0][i] = sum[0][i - 1] + d[0][i];
for (int i = 1; i < n; ++i)
for (int j = 1; j < m; ++j)
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + d[i][j];
}
void result() {
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
arr[i][j] += sum[i][j];
}
int main(void) {
add(0, 0, 2, 1, 3);
add(1, 1, 2, 2, -1);
pre_sum();
result();
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
cout << arr[i][j] << " ";
cout << endl;
}
return 0;
}
|
OJ例题
题目
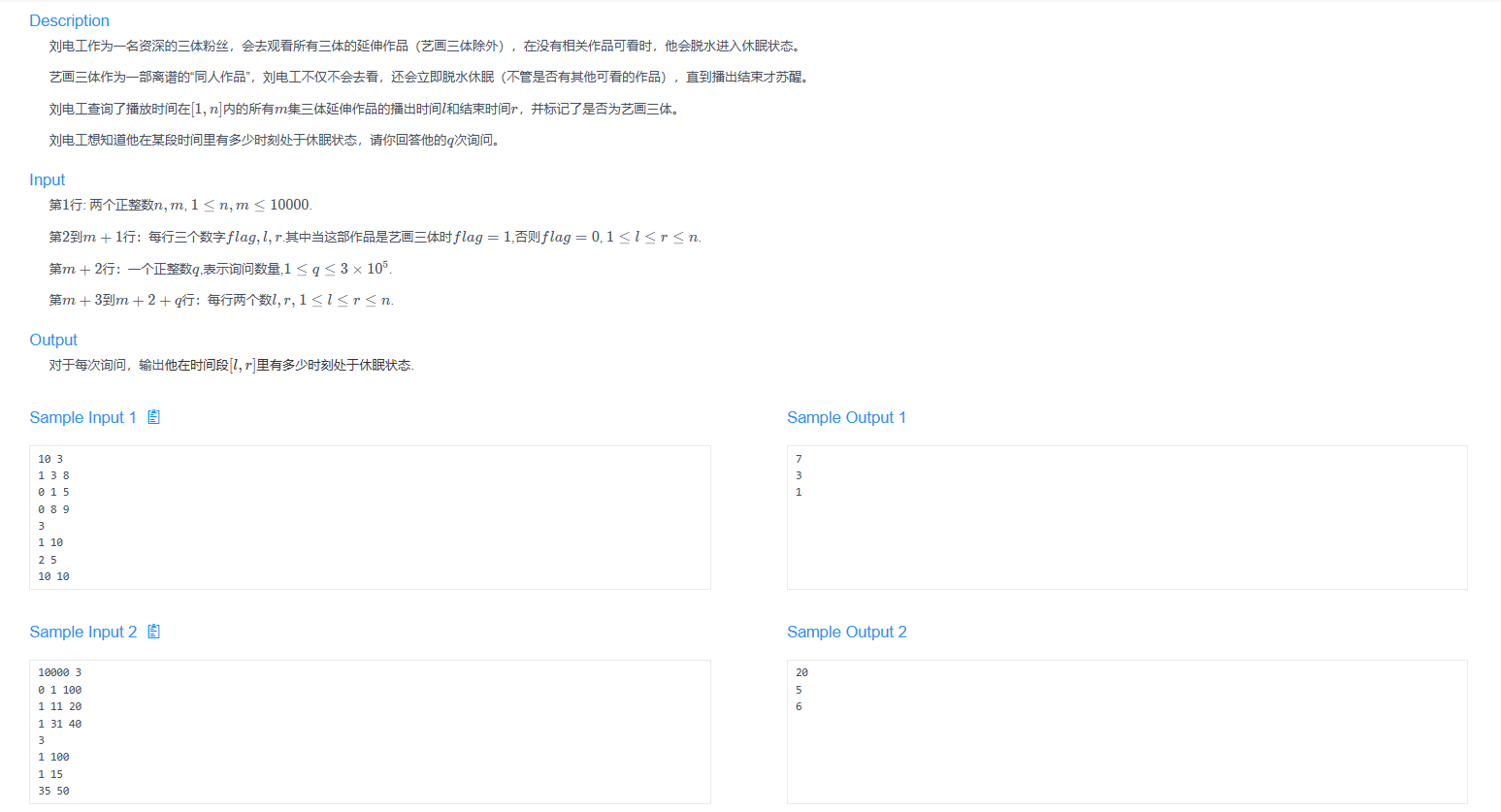
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include<iostream>
using namespace std;
const int N = 1e4 + 10;
int n, m, q, flag;
int d1[N], d2[N], d[N], sum[N];
int main(void) {
cin >> n >> m;
for (int i = 0; i < m; ++i)
{
int l, r;
cin >> flag >> l >> r;
if (flag == 0)
{
d1[l] += 1;
d1[r + 1] -= 1;
}
else
{
d2[l] += 1;
d2[r + 1] -= 1;
}
}
for (int i = 1; i <= n; ++i) {
d1[i] += d1[i - 1];
d2[i] += d2[i - 1];
if (d2[i] >= 1)
d[i] = 1;
else if (d1[i] >= 1)
d[i] = 0;
else
d[i] = 1;
sum[i] = sum[i - 1] + d[i];
}
cin >> q;
for (int i = 0; i < q; ++i)
{
int l, r;
cin >> l >> r;
cout << sum[r] - sum[l - 1] << endl;
}
return 0;
}
|
对于前缀和和差分还有其他类型以后待更新……