前置知识(不涉及证明)

欧几里得算法

欧几里得算法又称为辗转相除法，用于计算两个非负整数的最大公约数。对于非负整数a，b，当b不为0时，其最大公约数与非负整数b，a%b的最大公约数相同；当b为0时，a与b的最大公约数为a

1
2
3
long long gcd(ll a,ll b){
    return b?gcd(b,a%b):a;
}

裴蜀定理/贝祖定理

对于任意整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a，b是整数，且gcd(a,b)=d，那么对于任意的整数x，y而言ax+by都一定是d的倍数，特别地一定存在整数x，y使得ax+by=d成立

重要推论：a，b互质的充分必要条件是存在整数x，y使得ax+by=1

扩展欧几里得算法（exgcd）

  • 扩展欧几里德算法是用来在已知a，b 求解一组x，y ，使它们满足裴蜀（贝祖）等式：ax + by = gcd ⁡(a , b) = d

  • 证明过程：

    • 当b = 0时，ax + by = a因此x = 1，y = 0
    • 当b != 0时，经过以下推导

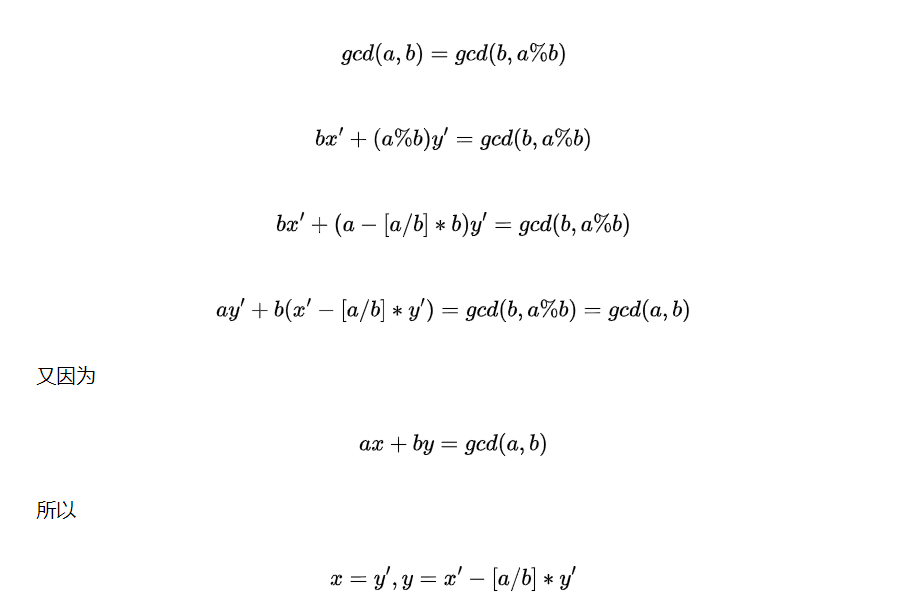
​ 因此可以利用递归算法每次先求出下一层的x’和y’然后利用上述公式回代

  • 递归方式模板
1
2
3
4
5
6
7
8
9
10
11
12
13
ll exgcd(ll a, ll b, ll &x, ll &y) {
  if (!b) {
    x = 1;
    y = 0;
    return a;
  }
  ll d = exgcd(b, a % b, x, y);
  ll t = x;
  x = y;
  y = t - (a / b) * y;
  return d;
}

应用

  1. 用于求解ax + by = gcd(a , b)的解（即上述情况）

  2. 用于求解ax + by = c的解

    • 当c % gcd(a , b) != 0时，无解（依据裴蜀定理）

    • 当c % gcd(a , b) = 0时，先利用exgcd求出ax + by = gcd(a , b)的解x0、y0，则可得到特解x’ = x0 * c / gcd(a , b)，y’ = y0 * c / gcd(a , b)，而通解 = 特解 + 齐次解（ax + by = 0的解），故通解为x = x’ + k * b / gcd(a , b)，y = y’ + k * a / gcd(a,b) (k为整数)

  3. 求解一次同余方程:

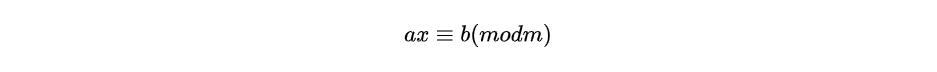
    上述方程价于

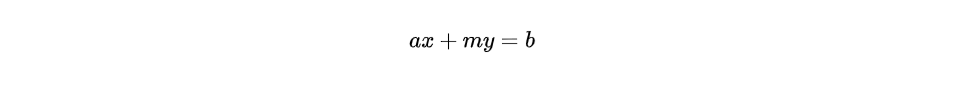
    再利用应用2中的方法求解即可

  4. 求解ax + by = c的最小正整数解x模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    LL ans=e_gcd(b,a%b,x,y);
    LL temp=x;
    x=y;
    y=temp-a/b*y;
    return ans;
}
 
LL cal(LL a,LL b,LL c)
{
    LL x,y;
    LL gcd=exgcd(a,b,x,y);
    if(c%gcd!=0) return -1;
    x*=c/gcd;//转化为a*x+b*y=c的解
    b/=gcd;//约去c后原来b就变为了b/gcd;
    if(b<0) b=-b;//如果b为负数就去绝对值
    LL ans=x%b;
    if(ans<=0) ans+=b;//求最小正整数解
    return ans;//返回的就是最小正整数解
}

参考文章

http://t.csdn.cn/SAzQN

http://t.csdn.cn/ZhE6r